Transformación de una función estándar a una general Ejercicio: 2) 01/02/13

INSTRUCCIONES:  Encontrar  la función general de la paravola que tiene vértice (3 , -5) y a= 2

1.- Se acomoda "a" y el vértice como en la formula:  y= a(x - h)² + k  y se identifican los términos: "a", "h", y "k":

a= 2 h= 3 k= 5

2(x - 3)² - 5 = f(x)

2.- Se resuelve el binomio al cuadrado:

2(x² - 6x + 9) -5 = f(x)

3.-  Se multiplica por 2 el resultado del binomio la cuadrado:

2x² - 12x + 18 -5 = f(x)

4.- Se suman los términos lineales:

2x² - 12x + 13 = f(x)

Cuando el coeficiente cuadratico es diferente de 1 Ejercicio 1) 31/01/13

INSTRUCCIONES: Transformar la siguiente función a forma estándar  graficar y poner  los elementos
y= 2x² - 12x + 19

1.- Se agrupa el termino cuadratico y el lineal:

[2x² - 12x] + 19

2.- Se factoriza lo que se agrupo tomando el termino cuadratico 

2[x² - 6x] + 19

3.- Se identifica el termino "b" del termino lineal, de todo lo que se encuentra en los corchetes para utilizar la formula: (b/2)² :

(b/2)² = (-6/2)² = (-3)² = 9

4.- Se suma y se resta el resultado de "b" dentro de los corchetes:

2[x² - 6x + 9 - 9] + 19

5.- Se factoriza para sacar el trinomio al cuadrado perfecto:

• Se saca el cuadrado del primer termino, se utiliza el símbolo del segundo termino, se saca la raíz del tercero y los demás se bajan tal como están:

               2[(x - 3)² - 9] + 19

6.- Se multiplica todo lo que esta dentro del los corchetes excepto el binomio al cuadrado por el 2:

               2(x-3)² - 18 + 19

7.- Se resuelve la operación que esta al lado del binomio al cuadrado:

  

             2(x - 3)² + 1

8.- Se identifican los terminos "a", "h", "k" y el vertice:

a= 2 h= 3 k= 1 V = (3 , 1)

9.- Se tabula:

X	Y
1	9
2	3
3	1
4	3
5	9

10.- Se grafica:

11.- Se anotan los elementos de la parabola:

Ramas	Arriva
Concavidad	Positiva
Vertice	(3 , 1)
Eje de simetría	3
Minimo	1

Convercion de formula general a forma estándar Ejercicio 3) 29/01/13

INSTRUCCIONES: de la siguiente función obtiene sus elementos y gráfica transformándolas a estándar
                             y= x² + 4x +1 

• Para la conversión se utiliza el método para completar un tcp (trinomio al cuadrado perfecto)

Se identifican los términos "a", "b" y "c":
      a= 1                   b=4                         c= 1
Se encuentra el vértice por medio de la formula: (b/2)²:

     (b/2)² = (4/2)² = 4

Se suma y se resta el resultado anterior a la función :
     y= x² +4x +4 -4 +1
Los primeros 3 términos que corresponden al tcp se factorizan para obtener un binomio al cuadrado:

• Se saca la raíz del primero, se utiliza el símbolo del segundo, se saca la raíz del tercero, se elevan al cuadrado formando un binomio la cuadrado, y los demás términos se ponen tal cual:

     (x + 2)² - 4 +1

• Se resuelven los términos que no están elevados al cuadrado:

     (x + 2)² - 3 

Se tabula de 0 a -4:

Se grafica:

Se anotan los elementos de la parabola

Ramas	Arriba
Concavidad	Positiva
Vertice	(-2,-3)
Eje de simetría	-2
Minimo	-3

Ecuación cuadrática de la forma estándar 25/01/13

1) y= x²

 2) y= 3x²

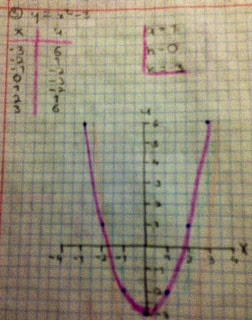
3) y = x² - 3

4) y= x²+3

5) y= ( x+ 3)²

6) y= (x - 3)²

Conclusiones:

·         Dependiendo de los valores de los términos “a”, “h” y “k” la gráfica se moverá.

·         Cuando “a” es positivo y vale 1 el vértice va en el origen,  las ramas son más cortas y van hacia arriba, y cuando es positivo y vale 3 el vértice va en el origen,  las ramas son más largas y van hacia arriba.

·         Cuando “h” es positivo la gráfica va a la derecha, y cuando es negativo va a la izquierda.

·         Cuando “k” es negativo el  vértice va hacia abajo y cuando es positivo va hacia arriba.