Investigación: Clasificación de ángulos

Ángulos llanos: Un angulo llano mide 180°.

Ángulos rectos: Es un angulo que mide exactamente 90°. si en la esquina del angulo hay un simbolo especial, una caja. si se ve este símbolo  el angulo es recto. Un angulo recto puede estar en cualqier orientacion o giro, lo que importa es que el angulo interior sea 90°.


Ángulos agudos: Angulo que mide menos de 90°

Ángulos obtusos: Angulo que mide mas de 90° pero menos de 180°

Ángulos adyacentes: Dos ángulos son adyacentes si tienen un lado y un vértice en común (esquina).

Ángulos opuestos por el vértice  Dos ángulos opuestos por el vértice son los ángulos opuestos cuando se cruzan dos lineas. Estos son congruentes.

Ángulos suplementarios: Dos ángulos son suplementarios si suman 180°.

Ángulos complementarios: Dos ángulos son complementarios si suman 90°

BIBLIOGRAFIA:

http://www.disfrutalasmatematicas.com

Punto medio y mediatriz de un segmento

Del segmento "C" localiza el punto medio y la mediatriz

Elementos geometricos

DIBUJA CUATRO RECTAS QUE SEAN CONCURRENTES

Transformación de una función estándar a una general Ejercicio: 2) 01/02/13

INSTRUCCIONES:  Encontrar  la función general de la paravola que tiene vértice (3 , -5) y a= 2

1.- Se acomoda "a" y el vértice como en la formula:  y= a(x - h)² + k  y se identifican los términos: "a", "h", y "k":

a= 2 h= 3 k= 5

2(x - 3)² - 5 = f(x)

2.- Se resuelve el binomio al cuadrado:

2(x² - 6x + 9) -5 = f(x)

3.-  Se multiplica por 2 el resultado del binomio la cuadrado:

2x² - 12x + 18 -5 = f(x)

4.- Se suman los términos lineales:

2x² - 12x + 13 = f(x)

Cuando el coeficiente cuadratico es diferente de 1 Ejercicio 1) 31/01/13

INSTRUCCIONES: Transformar la siguiente función a forma estándar  graficar y poner  los elementos
y= 2x² - 12x + 19

1.- Se agrupa el termino cuadratico y el lineal:

[2x² - 12x] + 19

2.- Se factoriza lo que se agrupo tomando el termino cuadratico 

2[x² - 6x] + 19

3.- Se identifica el termino "b" del termino lineal, de todo lo que se encuentra en los corchetes para utilizar la formula: (b/2)² :

(b/2)² = (-6/2)² = (-3)² = 9

4.- Se suma y se resta el resultado de "b" dentro de los corchetes:

2[x² - 6x + 9 - 9] + 19

5.- Se factoriza para sacar el trinomio al cuadrado perfecto:

• Se saca el cuadrado del primer termino, se utiliza el símbolo del segundo termino, se saca la raíz del tercero y los demás se bajan tal como están:

               2[(x - 3)² - 9] + 19

6.- Se multiplica todo lo que esta dentro del los corchetes excepto el binomio al cuadrado por el 2:

               2(x-3)² - 18 + 19

7.- Se resuelve la operación que esta al lado del binomio al cuadrado:

  

             2(x - 3)² + 1

8.- Se identifican los terminos "a", "h", "k" y el vertice:

a= 2 h= 3 k= 1 V = (3 , 1)

9.- Se tabula:

X	Y
1	9
2	3
3	1
4	3
5	9

10.- Se grafica:

11.- Se anotan los elementos de la parabola:

Ramas	Arriva
Concavidad	Positiva
Vertice	(3 , 1)
Eje de simetría	3
Minimo	1

Convercion de formula general a forma estándar Ejercicio 3) 29/01/13

INSTRUCCIONES: de la siguiente función obtiene sus elementos y gráfica transformándolas a estándar
                             y= x² + 4x +1 

• Para la conversión se utiliza el método para completar un tcp (trinomio al cuadrado perfecto)

Se identifican los términos "a", "b" y "c":
      a= 1                   b=4                         c= 1
Se encuentra el vértice por medio de la formula: (b/2)²:

     (b/2)² = (4/2)² = 4

Se suma y se resta el resultado anterior a la función :
     y= x² +4x +4 -4 +1
Los primeros 3 términos que corresponden al tcp se factorizan para obtener un binomio al cuadrado:

• Se saca la raíz del primero, se utiliza el símbolo del segundo, se saca la raíz del tercero, se elevan al cuadrado formando un binomio la cuadrado, y los demás términos se ponen tal cual:

     (x + 2)² - 4 +1

• Se resuelven los términos que no están elevados al cuadrado:

     (x + 2)² - 3 

Se tabula de 0 a -4:

Se grafica:

Se anotan los elementos de la parabola

Ramas	Arriba
Concavidad	Positiva
Vertice	(-2,-3)
Eje de simetría	-2
Minimo	-3

Ecuación cuadrática de la forma estándar 25/01/13

1) y= x²

 2) y= 3x²

3) y = x² - 3

4) y= x²+3

5) y= ( x+ 3)²

6) y= (x - 3)²

Conclusiones:

·         Dependiendo de los valores de los términos “a”, “h” y “k” la gráfica se moverá.

·         Cuando “a” es positivo y vale 1 el vértice va en el origen,  las ramas son más cortas y van hacia arriba, y cuando es positivo y vale 3 el vértice va en el origen,  las ramas son más largas y van hacia arriba.

·         Cuando “h” es positivo la gráfica va a la derecha, y cuando es negativo va a la izquierda.

·         Cuando “k” es negativo el  vértice va hacia abajo y cuando es positivo va hacia arriba. 

Análisis del discriminante: Ejercicio 2) 24/01/13

INSTRUCCIONES Graficar la siguiente función:
f(x) = - x² + 3x
1.- Se identifican los términos "a", "b" y "c":
a = -1
b = 3
c = 0
2.- Se factoriza la función para sacar el discriminante:
(-x + 3) (x + 0) = 0
-x + 3 = 0 x + 0 = 0
- x = - 3 x = 0
3.- Se saca el vértice por medio de la formula: -b / 2a:
x = -3 / 2 = 1.5
• Se sustituye en f(x):
f(x) = -(1.5)² + 3(1.5)
f(x) = 2.25 + 4.5
f(x) = 2.25
4.- Se grafica:

Puntos importantes de una parábola. Ejercicio b) 22/1/13

Instrucciones: Graficar la siguiente función cuadratica a partir del vértice y la dos raíces, con los elementos de la parábola:

b) f(x) = x² + 2x + 3

Para empezar a tabular se obtiene el punto "X" del vértice utilizando la fórmula: x = -b/2a

x = -2/2 (1)

x = -2/2

x = -1

Una vez que se encuentra el punto "x" se sustituye en la función f(x);

f(x) = (-1)² -2 (-1) -3
f(x) = 1 -2 -3

f(x) = -4

Para sacar las raíces faltantes se tiene que usar la formula general que es:

x 1, x 2 = -b ∓ √b² - 4 a c / 2a

x 1, x 2 = -2 ∓ √(2)² - 4 (1) (-3) / 2(1)

x 1, x 2 = -2 ∓ √4 + 12 / 2

x 1, x 2 = -2 ∓ √16 / 2

x 1, x 2 = -2 ∓ 4 / 2

x 1 = -2 + 4 / 2

x 1 = 2 / 2

x 1 = 1

x 2 = -2 - 4 / 2

x 2 = -6 / 2

x 2 = -3

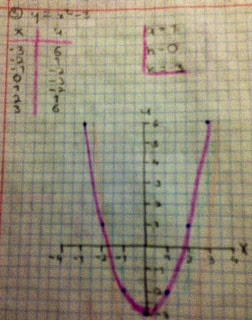
Una vez que se sacaron las raíces de x1, x2 y se acomodan los términos x1, x2, x y f(x) en la tabla:

Una vez que se acomodaron los términos x1, x2, x y f(x) se gráfica:

Una vez graficada la tabulación se anotan los elementos de la parábola:

Ramas: Arriba

Contabilidad: Positiva

Vértice: (-1, -4)

Eje de simetría: -1

Mínimo: -4

Ejercicio c) elementos de una parabola 18/01/13

INDICACIONES: OBTIENE LOS ELEMENTOS DE LA PARÁBOLA Y LA GRÁFICA DE LA FUNCIÓN: y = -x -x²

   1.       Se acomoda la ecuación de la forma: y(x) = ax² + bx + c

A(x) = - x² – x

   2.       Se identifican los términos:

a = -1

b = -1

c = 0

    3.       Una vez  identificados estos términos, se tabula:

x	y
-5	-30
-4	-21
-3	-14
-2	-9
-1	-6
0	-5
1	-6
2	-9
3	-14
4	-21
5	-30

    4.       Después de tabular se gráfica:

5.       Ya que se gráfico se obtienen los elementos de la parábola que son:

Ramas	Abajo
Concavidad	Negativa
Vértice	(0,-5)
Eje de simetría	0
Máximo	-5

Elementos de una párabola

• Eje de simetría: Recta vertical que divide a ésta en dos partes iguales.
• Vértice: Punto de corte de dicho eje con la parábola y tiene de coordenadas.
• Ramas: Abertura de la parábola, pueden  ser cóncavas hacia arriba o cóncava hacia abajo.
• Concavidad: El valor de  a nos indica el tipo de  concavidad  de la parábola:

Ø  Si a>0, es cóncava hacia arriba.

Ø  Si a<0, es cóncava hacia abajo.

• ·         Máximo o mínimo: El vértice es el punto máximo de una parábola cóncava hacia abajo y el punto mínimo de una parábola cóncava hacia arriba.
• 
  

Bibliografia:

·         http://www.aularagon.org/files/espa/ON_Line/matematicas/CMMC5Funciones/CMMC7Complementarias_3.htm

·         http://facultad.bayamon.inter.edu/edavila/Precalculo%201511/FUNCION%20CUADRATICA%20%20PRES%20%20MSP%2021.pdf

Ejercicio Funciones cuadráticas 17/01/13

Un granjero tiene 120m de malla de alambre y con ello desea cercar un terreno de forma rectangular. ¿Qué área puede cercar?

• Se saca la formula del perímetro que es:

       1.-  x + 2b = 120

• Se saca la formula del área que es:

       2.- A(x) = xb

• Se despeja ''b'' de la ecuación 1:

       2b = 120 - x

          b = 120 - x

                      2

          b = 60 - 1/2x

• Se sustituye ''b'' en la ecuación 2:

       A(x) = x (60 - 1/2x)

       A(x) = 60x - 1/2x²

• Ya sustituida la ecuación 2, se tabula:

X	Área
0	0
20	1000
40	1600
60	1800
80	1600
100	1000
120	0

• Una vez hecha la tabulación, se gráfica:

• Respuesta:

             El área del terreno que se puede cercar. 

             Va de 0 a 1800m²